Continuité et discontinuité

Natura non facit saltus
« La nature ne fait pas de sauts »
Leibniz

.Seul le néant est continu et n’a pas d’inverse.
René Lebon

CONTINUITE ET DISCONTINUITE

La continuité est le fait de toujours pouvoir mettre un autre point entre deux points. C’est une opération infinie. On a un bon exemple avec la démonstration de Nicolas de Cues qui montre dans son livre la « Docte ignorance » que le cercle est l’aboutissement de polygones inscrits et circonscrits en multipliant indéfiniment leurs côtés. Le cercle est un inaccessible qui sert à démontrer que la recherche de la coïncidence d’opposés est sans fin. C’est comme considérer le milieu d’un segment en prenant continuellement le milieu du segment restant. L’issue ne pourrait être que 0 qui n’est jamais atteint qu’à la suite d’opérations en nombre infini. Le 0 et l’∞ se rejoignent.

La discontinuité est différente. Il s’agit par exemple de considérer des points équidistants sur une droite avec un intervalle constant, comme les raies de Zeemann. Dans un atome, les électrons ne s’alimentent en énergie que par paquets qui modifient leurs orbites de présence qui sont ainsi discontinues.

La discontinuité se retrouve dans la monnaie. Une somme d’argent n’est surtout mesurable qu’à partir du moment où elle est constituée de portions égales. Il y a un moyen terme car si ces portions sont trop importantes cela n’est pas très manipulable. De même, si elles sont petites, il en faudrait une grande quantité. Dans les bilans comptables on a choisi le centime ce qui donne des résultats interprétables facilement. Il ne serait pas très pratique d’avoir des milliardièmes de milliardièmes d’euros comme unité de base. Le problème s’est posé pour définir la quantité d’énergie que recèle un système. Si l’on veut compter l’énergie par morceaux on est aidé par le principe de l’équipartition de l’énergie pour chaque composant. Comme pour la monnaie il faut choisir ce morceau d’énergie de taille la plus réduite possible. L’énergie est représentée par des ondes de fréquences diverses et échelonnées graduellement. Mais dans ce cas la fréquence augmente régulièrement sans limite. L’énergie soit la température peut être infinie même si elle se réduit à tangenter le 0 sans jamais l’atteindre. Les résultats sont mauvais si les fréquences sont basses. C’est la formule de Rayleigh-Jeans qui conduit à la catastrophe ultraviolette. Wien met au point une formule convenant mieux aux hautes fréquences, fonction des données expérimentales.

La thèse de l’équipartition de l’énergie suivant certains niveaux a été formulée par Boltzmann où le nombre de particules ayant l’énergie E_i est N_i = exp-E_i/kT, kT étant l’énergie maximum du système. Le système imaginé par Planck est de tapisser les parois de la cavité d’oscillateurs (une prémonition de l’atome). Mais il postule que les oscillations ne sont pas continues mais procèdent par petites saccades, fonction de la fréquence f de l’oscillateur. Pour cela il suffit d’appliquer un coefficient constant à un écart très petit des fréquences supposées continues. Planck triture la formule de Wien en cherchant des coefficients donnant un résultat conforme aux données expérimentales.

L’énergie se répartit équitablement selon l’hypothèse de Boltzmann en très petites quantités hf, telles qu’elles ne sont pas détectables en physique classique. On peut prendre l’image de l’échelle, plus la distance entre les barreaux est faible plus c’est facile d’y grimper mais il ne peut y avoir un nombre de barreaux infini.

C’est le spin qui apporte la discontinuité. Nous verrons que le spin, énergie intrinsèque de rotation d’un être quantique se mesure aussi en très faible quantité : ħ/2 = h/4π ce qui va conduire à n’avoir que deux classes d’êtres quantiques individuels : les bosons et les fermions.

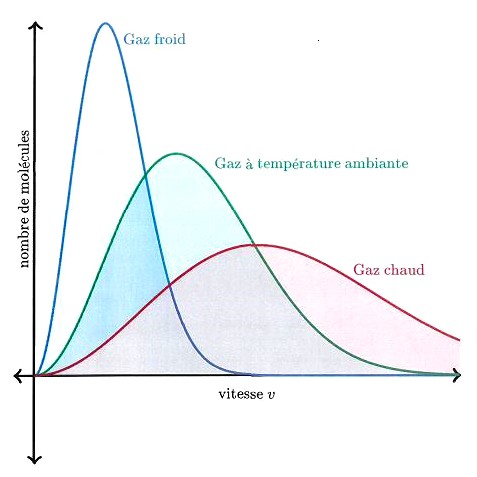
Il y a une très forte analogie entre les courbes de distribution de vitesse d’une particule selon Maxwell.

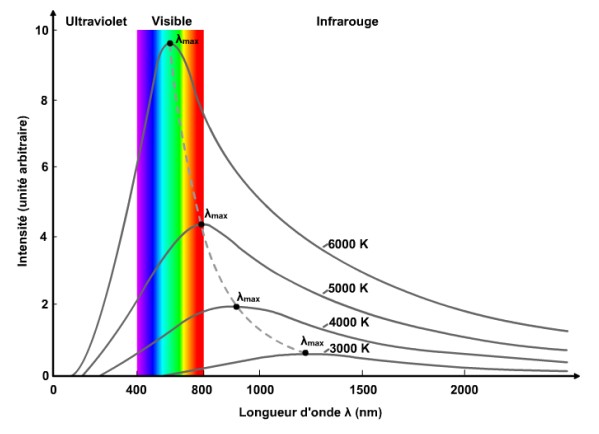
Les courbes de Planck ont pour abscisse la longueur d’onde. On peut faire aussi le rapprochement onde- particule, grand mystère de la mécanique quantique très difficile à admettre pour un esprit forgé au principe de non-contradiction d’Aristote.

Le renflement de la courbe est dû à ce que la quantité correspondant en abscisse est la plus probable. Les courbes partent du voisinage de 0 pour atteindre un maximum qui se réduit au fur et à mesure que la courbe se rapproche asymptotiquement de l’abscisse. Notons que les courbes à différentes températures se superposent en restant dans un espace euclidien ou complexe.

Reste l’énigmatique -1 dans le dénominateur de la formule de Planck. Disons que pour –1 il s’agit de bosons et pour +1 de fermions. Nous expliquerons cela dans l’article : Distribution de Maxwell –Boltzmann, de Fermi-Dirac et de Bose-Einstein.

L’action est ainsi comptabilisée en unités h. Il va y avoir autour de h une formidable explosion de découvertes qui vont rendre le monde quantique microscopique intelligible.

La continuité c’est-à-dire les barreaux de l’échelle confondus mènerait à une superposition continue de fréquences et à la catastrophe ultraviolette.

La discontinuité, c’est parsemer avec des boursouflures espacées de telle façon que cela puisse être compréhensible et heuristique. La nature est-elle réellement continue ? C’est l’homme qui l’aurait balisé avec des petites quantités à la limite du détectable. On ne peut strictement rien faire de la continuité. Nous ne comprenons que des différences en les réduisant le plus possible pour simuler la continuité. On ne « sait » que par différences ce qui n’est pas le cas de la continuité. L’idée d’Einstein est que c’est justement l’onde électromagnétique qui est sous forme de granulés à la limite du ponctuel nommés photons. Une onde monochromatique  continue n’apporte aucune information.

On peut dire que grâce à son acharnement Planck a permis de trouver le photon, à la fois particule et onde, et la découverte du spin.

La nature est-elle continue ? Mais comme elle n’est que ce que l’on en perçoit c’est le cerveau qui, pour mieux appréhender, apporte cette discontinuité qui donne la possibilité de compter, sans laquelle rien n’existe. L’utilisation constante et répétée de h permet de disséquer notre entourage et de le découper en très fines tranches. C’est une brisure de symétrie et d’harmonie.

C’est à partir de la discontinuité que se singularisent les êtres quantiques.

Cela est-il dû à un seuil d’excitabilité des neurones ?

Est-ce que en deçà de h, c’est le flou, l’indéterminé comme le laisse penser le mur de Planck qui détermine les limites au-delà desquelles plus rien n’est perceptible ? La constante de Planck h est très proche de zéro, mais elle n’est pas zéro.

Le zéro est un pôle attractif que l’on pourrait éventuellement atteindre que par une régression à l’infini. Toute chose veut y trouver le repos absolu mais elle en est refoulée pour préserver le statut de néant.

h est l’initiale de « hilfe » qui en allemand signifie en quelque sorte, à l’aide, au secours. Il est certain que Planck n’a pas perçu l’ampleur de sa découverte. Il a déclenché sans s’en rendre compte tout ce qui allait constituer le monde quantique.

Pourquoi h est-elle une constante ? Parce qu’il s’avère que le rapport entre l’énergie du photon et sa fréquence, c’est-à-dire sa répétition en une seconde, ne change pas. C’est en fait l’amplitude de l’onde qui reste identique. Elle est extrêmement faible. C’est la raison pour laquelle on ne la perçoit pas. Comment Planck avec ses appareils de mesure de l’époque a-t-il pu l’apprécier ?

Comme nous l’avons déjà dit, l’être quantique est, à la fois, onde et particule, notion qui est hors de portée de notre intellect. Ceci est plus ou moins résolu en considérant séparément particule et onde. C’est ce qui a été fait d’une part par Heisenberg qui voulait ne tenir compte des mesures que sous forme de groupes de nombres ou matrices. Mais, horreur, il s’aperçoit que le résultat du produit de la position spatio-temporelle  (q) et de l’impulsion mv (p) est différent suivant l’ordre avec lequel on effectue ce produit. Ceci, est, au contraire, au fondement de la mécanique quantique comme c’est indiqué dans l’article sur la non-commutativité. Par contre Schrödinger crée la mécanique ondulatoire par la fonction d’onde. Il donne à l’onde les propriétés de la continuité. Ceci a l’avantage de la considérer comme dérivable c’est-à-dire de définir sa limite lorsque les variables espace et temps tendent vers zéro. Le calcul est alors plus facile à exprimer que le calcul matriciel. Dirac les mettra d’accord en disant que ce sont deux aspects différents d’une même réalité (particule et onde).

En fait, à l’image du sablier, pour que le temps s’écoule, il faut que les gouttes d’énergie soient les plus petites possibles. C’est à cette condition que tout bouge dans une valse effrénée pour essayer d’atteindre l’inaccessible repos du néant.

Un bel exemple de discontinuité est le sablier. Les grains de sable pour passer d’un compartiment à l’autre par le goulot d’étranglement doivent avoir une certaine taille. Elle ne peut bien sûr être nulle. Elle doit permettre aux grains de sable de glisser les uns sur les autres. Pour cela la taille doit être régulière car alors un gros grain empêcherait les petits de passer. Les grains doivent avoir la plus petite taille possible. C’est ce que fait la nature avec sa moindre action possible. L’action ne peut être inférieure à ħ/2.

Ajoutons que le sablier est censé mesurer le temps ce qui conduit à penser que ce temps ne s’écoule que si les grains d’énergie (les photons) sont les plus petits possibles.

Autre exemple : la transformée de Fourier qui est une superposition d’ondes de fréquences multiples de nombres entiers qui sont les nœuds. Il ne peut y avoir continuité sans la possibilité de discontinuité et vice versa.

La discontinuité est une brisure de la continuité, une boursouflure du néant > ħ/2 qui se propage et se superpose à d’autres boursouflures.

Le paradoxe de la flèche de Zénon illustre bien la discontinuité. Au départ elle est sur un arc tendu prête à se diriger vers un but lorsqu’elle est lâchée. C’est l’instant t₀. Pour qu’il y ait mouvement il faut qu’au temps t₁ elle ait parcouru un certain  espace. S’il y a continuité, cela signifie que la flèche doit d’abord être à quelque endroit à l’instant t₁/2. Puis également au temps t₁/4. Mais il lui faut toujours la moitié du temps pour se mouvoir, donc la flèche ne bougera pas. Elle reste immobile. Par contre s’il y a discontinuité elle peut parcourir des espaces extrêmement petits. Ils sont si faibles que l’on a l’illusion de la continuité et la flèche peut atteindre son but. Mais en fait la flèche n’avance que par saccades indétectables.

Dans ce sens on peut dire qu’il n’y a pas de réalité. Le mouvement n’est qu’illusion, « é como nullo », comme le dit Galilée, puisqu’il n’est qu’une succession d’actions extrêmement faibles.

La continuité est monotone. C’est la non-vie. Pour qu’il y ait vie il faut de la différence. C’est ce qu’apporte la discontinuité. Elle doit être très ténue pour donner l’apparence de la parfaite symétrie. On ne peut parfaire le polissage d’un miroir qu’en utilisant des grains abrasifs de plus en plus fins.

Cette extraordinaire découverte de Planck complétée par Einstein va être la source de toute la physique quantique et nous permettre une connaissance plus approfondie du comportement des objets quantiques à l’échelle microscopique

La discontinuité est plus économe en dépense d’action que la continuité… Un système de transistors fonctionne sur « tout ou rien », le courant électrique « passe » ou « ne passe pas », cela étant commandé par un faible signal électrique qui est comme un interrupteur (allumé, éteint).

Pour passer un flux d’énergie par une porte de façon la plus économe possible vaut-il mieux que la porte soit ouverte ou fermée ou faut-il entrouvrir la porte de manière à ce que le flux passe constamment et progressivement ? Dans le dernier cas il y a obstruction donc frottement. C’est par conséquent plus coûteux.

Nous avons vu que la discontinuité était préférable à la continuité à la condition qu’elle soit extrêmement faible. Ainsi elle économise l’action.

Tout cela répond parfaitement à ce que l’on appelle le principe de moindre action. La nature recherche à faire le moins d’effort possible. C’est cette faible discontinuité réduite au bit d’information qui permet la différence sans laquelle on ne pourrait connaître.  Le continu est inconnaissable.  Il y a une valeur optimale pour la « constante » de Planck vers laquelle on tend et où elle est constamment ramenée.

Les transistors, s’ils figurent bien le couple dualiste {0,1} sont également économes en énergie. Le transistor est certainement la plus grande invention humaine et la plus extraordinaire.

Nous verrons dans la deuxième partie dédiée au spin que ce dernier est tout à fait adéquat pour représenter la plus petite discontinuité possible (± ħ/2). h n’est qu’une forme de cette discontinuité. Le spin n’est pas comme le transistor une invention humaine, il est intrinsèque à la nature.

Fiat lux « que la lumière soit et la lumière fut »

La genèse figure le monde comme une sorte de combat entre les ténèbres et la lumière. Peut-être peut-on y voir une forme d’opposition et de complémentarité entre ces deux ingrédients ? Les ténèbres sont une image de la continuité alors que l’on sait que la lumière est discontinue par les photons qui dissipent l’obscurité à la vitesse c tout en ne pouvant pas se scinder et parvenir au néant que représenteraient les ténèbres.

Un bel exemple de discontinuité est le compact disc (CD) constitué par une succession de petits trous provoqués par un laser. La lecture de ces nombreux trous par le laser permet de donner à la musique l’impression d’une continuité.